반응형
SMALL
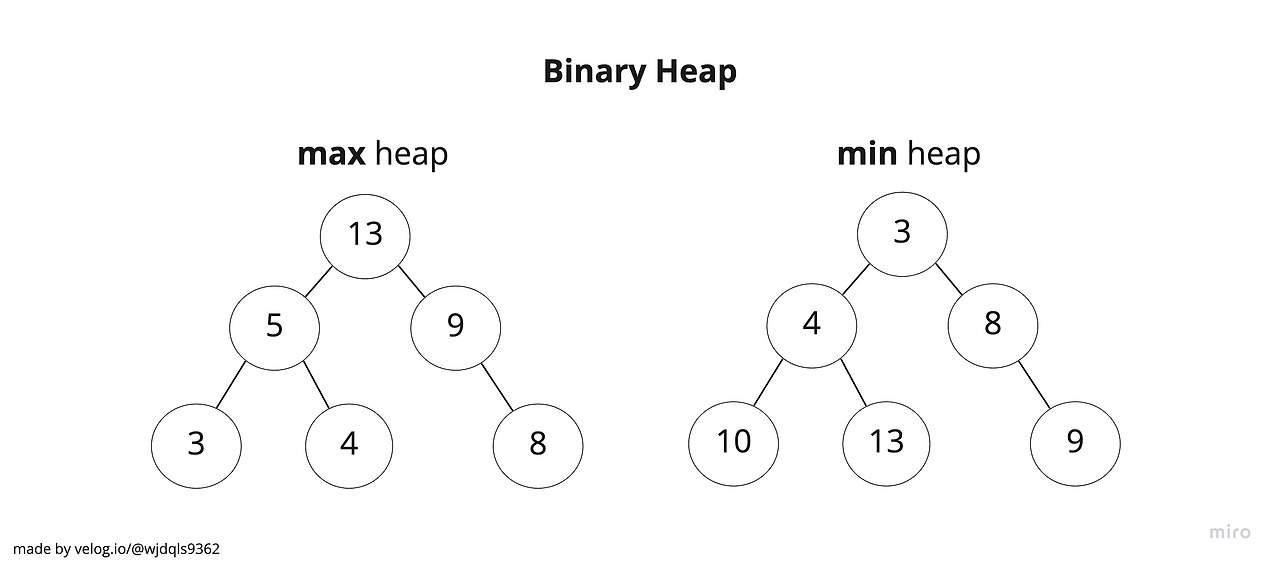
이진 힙(Binary Heap)은 완전 이진 트리를 기반으로 하는 자료 구조로, 주로 우선순위 큐를 구현하는 데 사용됩니다. 이진 힙은 크게 두 종류로 나뉩니다: 최소 힙(Min Heap)과 최대 힙(Max Heap)입니다. 최소 힙에서는 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 같아야 하며, 최대 힙에서는 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크거나 같아야 합니다. 이로 인해 이진 힙의 루트 노드는 전체 트리에서 최소값(최소 힙의 경우) 또는 최대값(최대 힙의 경우)을 가지게 됩니다.
이진 힙을 자바스크립트로 구현하는 것은 배열을 사용하여 비교적 간단합니다. 힙 내의 각 요소들은 일련의 연산을 통해 관리되며, 주로 다음 네 가지 주요 연산을 구현합니다:
- 삽입(Insert): 새로운 요소를 힙에 추가합니다. 새 요소는 먼저 힙의 마지막에 추가된 후, 힙의 조건을 만족시키기 위해 적절한 위치로 이동합니다.
- 삭제(Delete): 힙에서 최소값(최소 힙의 경우) 또는 최대값(최대 힙의 경우)을 제거합니다. 보통 루트 노드가 제거되며, 이후 힙의 재구성이 이루어집니다.
- 힙 구성(Heapify): 주어진 배열을 이진 힙 조건을 만족하는 형태로 재구성합니다. 주로 삭제 연산 후 또는 초기 힙 생성 시 사용됩니다.
- 피크(Peek): 힙의 최소값 또는 최대값을 조회합니다. 힙에서 요소를 제거하지 않고 값만 반환합니다.
다음은 최소 힙을 구현한 간단한 자바스크립트 예제 코드입니다:
class MinHeap {
constructor() {
this.heap = [];
}
getParentIndex(i) { return Math.floor((i - 1) / 2); }
getLeftChildIndex(i) { return 2 * i + 1; }
getRightChildIndex(i) { return 2 * i + 2; }
// 요소 삽입
insert(key) {
this.heap.push(key);
this.heapifyUp();
}
// 상향식 힙 구성
heapifyUp() {
let index = this.heap.length - 1;
while (this.getParentIndex(index) >= 0 && this.heap[this.getParentIndex(index)] > this.heap[index]) {
let parentIndex = this.getParentIndex(index);
[this.heap[parentIndex], this.heap[index]] = [this.heap[index], this.heap[parentIndex]];
index = parentIndex;
}
}
// 힙에서 최소값 제거 및 반환
extractMin() {
const min = this.heap[0];
this.heap[0] = this.heap.pop();
this.heapifyDown();
return min;
}
// 하향식 힙 구성
heapifyDown() {
let index = 0;
while (this.getLeftChildIndex(index) < this.heap.length) {
let smallerChildIndex = this.getLeftChildIndex(index);
if (this.getRightChildIndex(index) < this.heap.length && this.heap[this.getRightChildIndex(index)] < this.heap[smallerChildIndex]) {
smallerChildIndex = this.getRightChildIndex(index);
}
if (this.heap[index] < this.heap[smallerChildIndex]) {
break;
}
[this.heap[index], this.heap[smallerChildIndex]] = [this.heap[smallerChildIndex], this.heap[index]];
index = smallerChildIndex;
}
728x90
반응형
LIST
'algorithm > 자료구조' 카테고리의 다른 글
| 그래프 (0) | 2024.03.20 |
|---|---|
| 우선순위 큐(Priority Queue)와 덱(Deque) (0) | 2024.03.20 |
| DFS, BFS, 트리 순회(traversal) (0) | 2024.02.25 |
| remove : 이진탐색트리(Binary Search Tree, BST) (0) | 2024.02.25 |
| search : 이진탐색트리(Binary Search Tree, BST) (0) | 2024.02.25 |