반응형
SMALL
이진 트리는 각 노드가 최대 두 개의 자식 노드를 가질 수 있는 트리 구조입니다. 일반적으로 이진 트리는 검색, 정렬, 데이터 저장 등 다양한 컴퓨터 과학 문제를 해결하는 데 사용됩니다.
이진 트리의 다양한 종류 중에
"Full Binary Tree",
"Perfect Binary Tree",
"Complete Binary Tree",
"Degenerate (or Pathological) Binary Tree",
"Balanced Binary Tree"
들은 각각 고유한 특성을 가지고 있지만, 몇 가지 공통적인 유사점도 공유합니다. 여기서는 이 다섯 가지 이진 트리 유형의 주요 특징과 함께 그들이 공유하는 유사점에 대해 설명합니다.
주요 특징
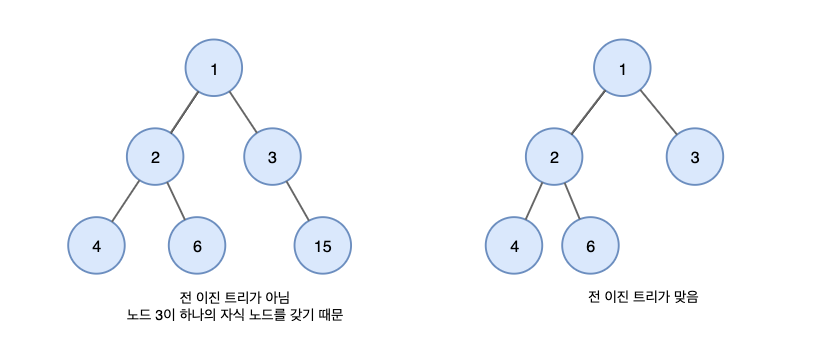
- Full Binary Tree: 모든 노드가 0개 또는 2개의 자식 노드를 가집니다.
출처 : https://yoongrammer.tistory.com/69
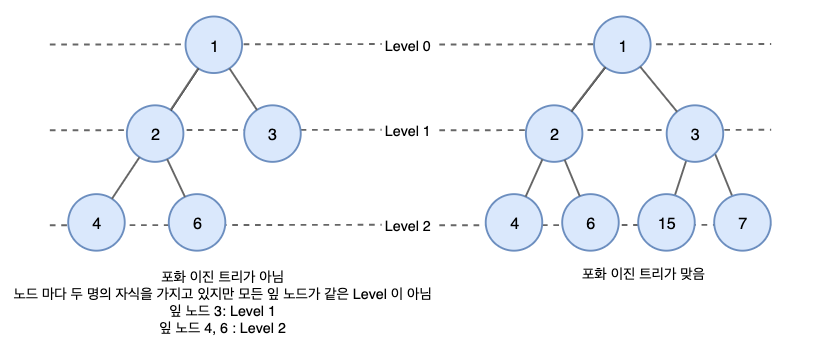
- Perfect Binary Tree: 모든 레벨이 완전히 채워져 있으며, 모든 리프 노드는 같은 깊이를 가집니다.
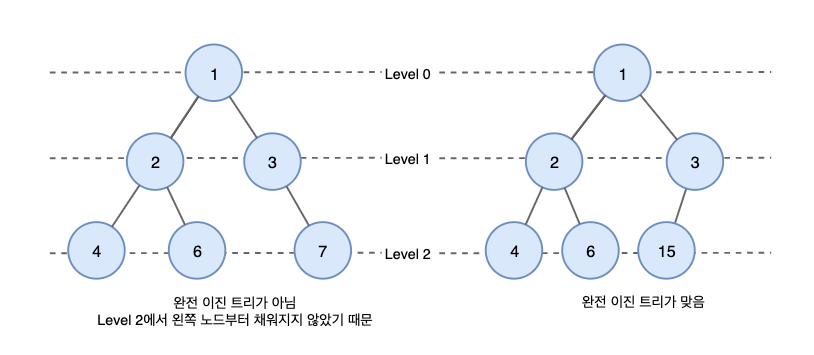
- Complete Binary Tree: 모든 레벨이 완전히 채워져 있으며, 마지막 레벨을 제외하고. 마지막 레벨은 왼쪽부터 차례대로 채워집니다.
- Degenerate (or Pathological) Binary Tree: 각 노드가 하나의 자식만 가지는 경우로, 사실상 연결 리스트와 같은 형태입니다.
- Balanced Binary Tree: 노드의 두 서브트리 간의 높이 차이가 일정 기준(보통 1 또는 2)을 넘지 않아 검색, 삽입, 삭제 연산이 효율적으로 수행됩니다.
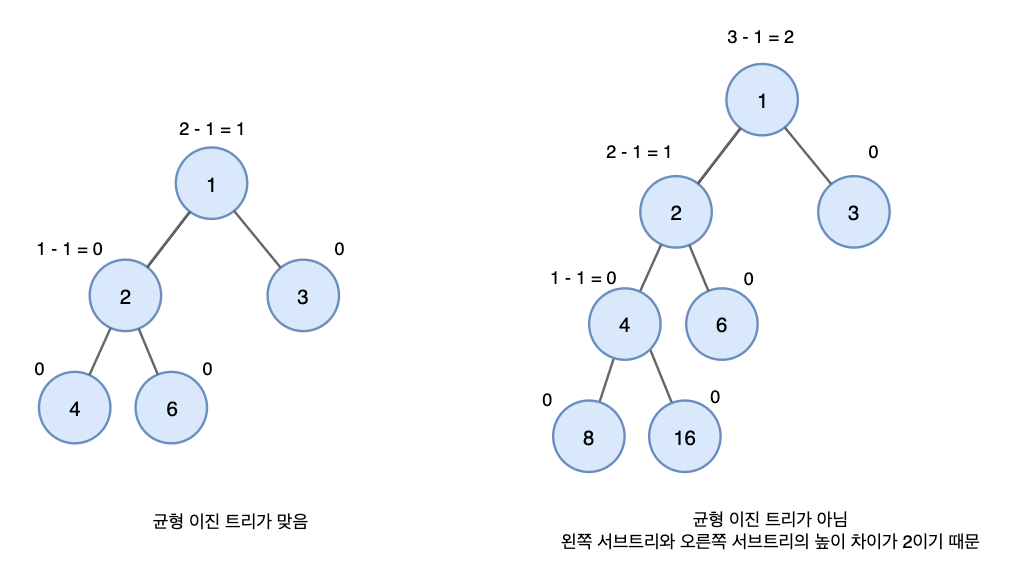
공통 유사점
- 이진 트리 구조: 모든 유형이 기본적으로 이진 트리 구조를 따릅니다. 즉, 각 노드는 최대 두 개의 자식(왼쪽 및 오른쪽)을 가질 수 있습니다.
- 재귀적 특성: 각 이진 트리는 재귀적으로 정의될 수 있으며, 작은 서브트리도 동일한 속성을 가지는 이진 트리입니다.
- 트리 순회: 전위 순회(pre-order), 중위 순회(in-order), 후위 순회(post-order), 그리고 레벨 순서 순회(level-order)와 같은 트리 순회 방법을 사용하여 트리의 모든 노드를 방문하고 검색할 수 있습니다.
- 동적 데이터 구조: 데이터의 추가, 삭제, 검색 등을 위해 동적으로 조정될 수 있습니다. 특히, 노드의 추가나 삭제 시에는 트리의 구조가 변경될 수 있습니다.
- 데이터 저장과 검색: 모든 유형의 이진 트리는 데이터 저장과 검색을 위한 구조를 제공합니다. 특히, 이진 탐색 트리(BST)는 이러한 목적에 매우 적합합니다.
- 알고리즘과 자료 구조: 컴퓨터 과학에서 다양한 문제를 해결하기 위한 알고리즘과 자료 구조로 널리 사용됩니다. 각 유형의 트리는 특정 알고리즘에 최적화되어 있습니다.
이러한 유사점은 모든 이진 트리가 공유하는 기본적인 속성과 기능을 반영합니다. 각 트리 유형은 특정 애플리케이션 또는 연산의 요구 사항에 따라 선택되어야 합니다.
728x90
반응형
LIST
'algorithm > 자료구조' 카테고리의 다른 글
| search : 이진탐색트리(Binary Search Tree, BST) (0) | 2024.02.25 |
|---|---|
| insert : 이진탐색트리(Binary Search Tree, BST) (0) | 2024.02.25 |
| 스택(Stack), 큐(Queue), 트리(Tree) (0) | 2024.02.22 |
| 연결 리스트에서 노드(Node)란? (0) | 2024.02.16 |
| 연결리스트의 시간복잡도 (1) | 2024.02.09 |